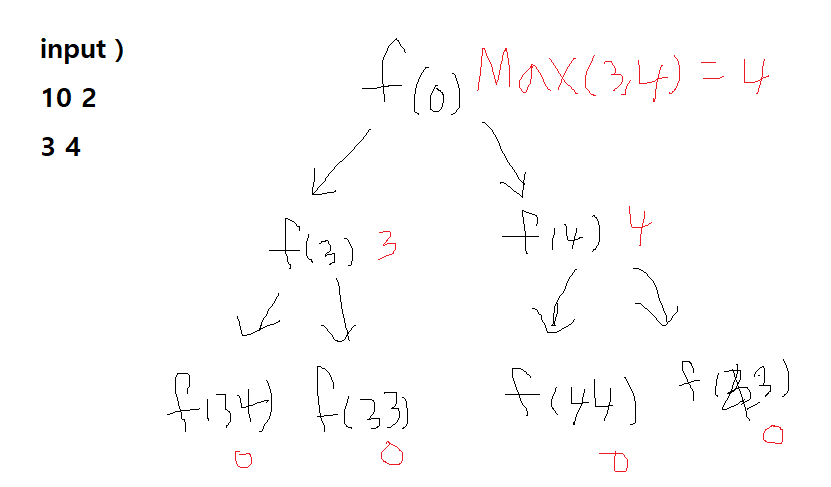- 문제 : https://www.acmicpc.net/problem/2805

- 분류 : 이분탐색

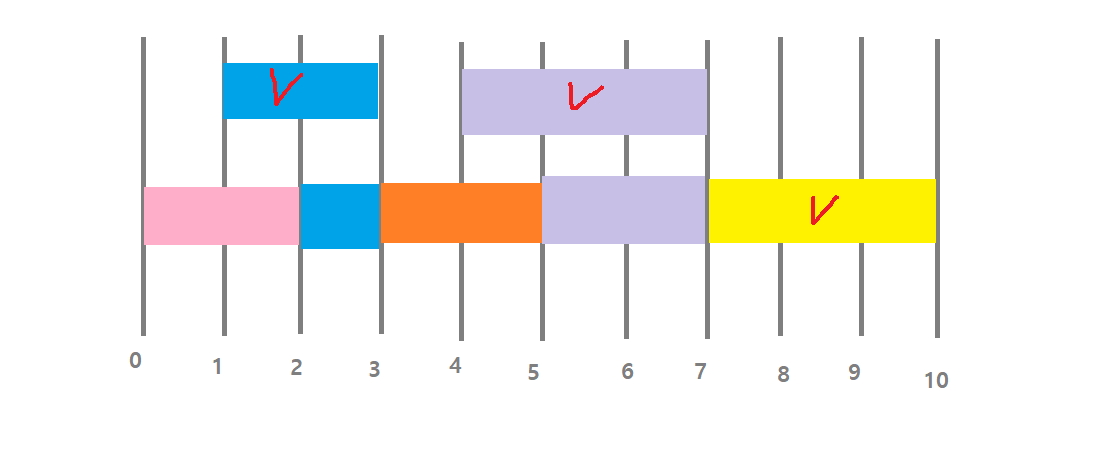
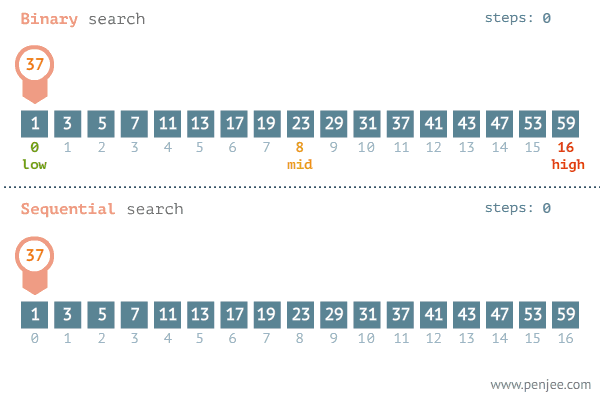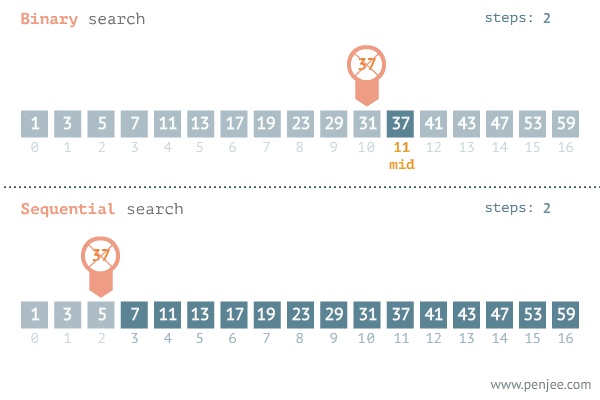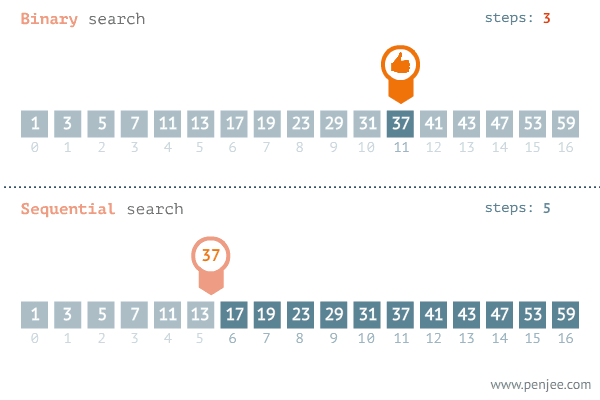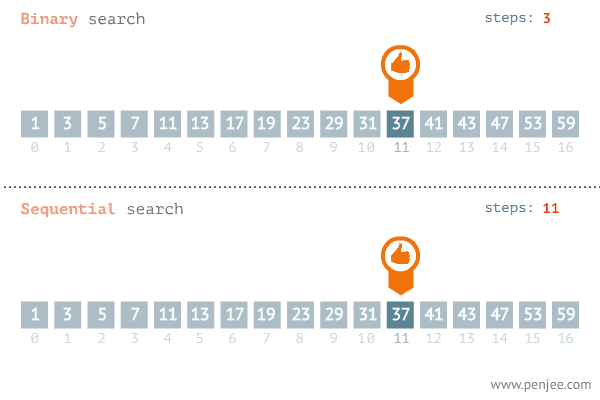
이분탐색 (Binary Search)

이분탐색 알고리즘은 linear search에서 업그레이드된 방식으로, 정렬된 리스트를 반으로 나눠서 반복 탐색하는 방식이다.

계속 탐색범위를 반으로 나누므로 시간복잡도는 O(logN)이다.

백준2805번 나무자르기 풀이

• 나무의 높이의 합은 항상 M보다 크거나 같기 때문에, 상근이는 집에 필요한 나무를 항상 가져갈 수 있다. => 상근이가 나무를 집에 가져가지 못할 경우는 없다. (즉 탐색했을 경우 찾는 값이 없는 경우는 없다)
  • if(first > last) return null;  not found 인 경우는 없다.
• 나무의 높이는 1,000,000,000보다 작거나 같은 양의 정수 또는 0이다 => 가져갈 나무의 높이의 합을 구할 때 int 범위를 초과할 수 있으므로 result는 long타입으로 설정한다. 
  • int형 저장범위 : -2,147,483,648 ~ 2,147,483,647
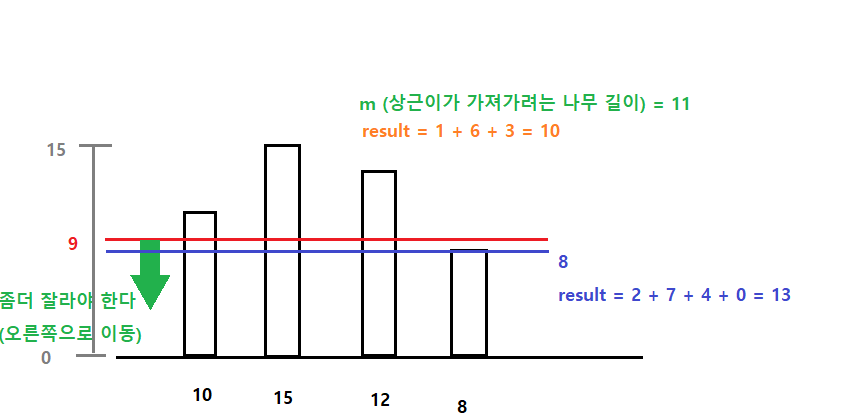
• 높이가 H보다 큰 나무는 H 위의 부분이 잘릴 것이고, 낮은 나무는 잘리지 않을 것이다. => (나무의 높이 - h)가 음수인 경우는 잘리지 않기 때문에 result에 더하지 않는다. 
• 0부터 최대 나무의 높이를 범위로 두고, 이분탐색으로 절단기에 설정할 수 있는 높이의 최댓값을 구한다.
  • 만약 result < m 이면 더 잘라야하므로 왼쪽 범위를 탐색한다 (좀더 자르려면 절단기의 높이가 낮아져야 한다)
  • result > m 이면 덜 잘라야하므로 오른쪽 범위를 탐색한다 (좀덜 자르려면 절단기의 높이를 높혀야 한다)

import java.util.Arrays;
import java.util.Scanner;

public class BOJ2805 {

    static int[] trees;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int n = sc.nextInt();
        int m = sc.nextInt();
        sc.nextLine();
        trees = new int[n];
        for (int i = 0; i < n; i++) {
            trees[i] = sc.nextInt();
        }

        int first = 0;
        int last = Arrays.stream(trees).max().getAsInt(); //최대 높이의 나무
        int middle = (last + first) / 2;
        long result = findResult(middle);

        while (first <= last) {
            if (result < m) {
                // 더 조금 잘라야 하니 왼쪽으로
                last = middle - 1;
            } else {
                // 더 많이 잘라야 하니 오른쪽으로
                first = middle + 1;
            } 

            middle = (last + first) / 2;
            result = findResult(middle);
        }
        System.out.println(middle);
    }

    public static long findResult(int h) {
        long result = 0;
        for (int tree : trees) {
            //음수인 경우는 더하지 않는다
            result += (Math.max((tree - h), 0));
        }
        return result;
    }
}

나무자르기 테스트케이스

1 1
1000000000
output : 999999999

5 100
99 1 1 1 1
output : 0

• 문제 : https://www.acmicpc.net/problem/17609
• 분류 : 투포인터 
• 시간초과를 해결하기 위해 check가 2 이상인 경우는 바로 2를 리턴해준다. 이미 회문, 유사회문이 아닌 것으로 판정났으니 더이상 재귀함수를 호출하지 않도록.
• 풀이방법 : 투포인터로 문자열의 맨앞부터 시작, 문자열의 맨뒤부터 시작해서 서로 비교한다. 만약 서로 다른 구간이 발생하면 그 앞뒤로 비교하도록 하고, 만약 앞뒤로 비교했을 때 회문으로 충족된다면 유사회문으로 볼 수 있다.

package boj.string;

import java.io.BufferedReader;
import java.io.InputStreamReader;

/**
 * @문제명 회문
 * @분류 투포인터, 문자열
 */
public class BOJ17609 {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());

        String[] arr = new String[n];
        for (int i = 0; i < n; i++) {
            arr[i] = br.readLine();
        }

        for (int i = 0; i < n; i++) {
            String current = arr[i];
            System.out.println(palindrome(0, current.length() - 1, current, 0));
        }
    }

    private static int palindrome(int s, int e, String s1, int check) {
        // 시간초과를 해결하기 위해 아래 조건을 추가함
        if(check >=2) return 2;

        while (s < e) {
            if (s1.charAt(s) == s1.charAt(e)) {
                s++;
                e--;
            } else {
                return Math.min(palindrome(s + 1, e, s1, check + 1), palindrome(s, e - 1, s1, check + 1));
            }
        }
        return check;
    }
}

<ul style="list-style-type: disc;" data-ke-list-type="disc">
<li>분류 : 완전탐색, 재귀</li>
<li>풀이</li>
</ul>
<p>

</p>
<pre id="code_1682592342876" class="java" data-ke-language="java" data-ke-type="codeblock"><code>import java.util.Arrays;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int count = sc.nextInt();
        sc.nextLine();
        int[] k = new int[count];
        for (int i = 0; i &lt; count; i++) {
            k[i] = sc.nextInt();
        }

        Arrays.sort(k);

        int result = find_max(n, k, 0);
        System.out.println(result);

    }

    private static int find_max(int n, int[] k, int currentMax) {
        if(currentMax &gt; n) return 0;
        int max = currentMax;
        for (int i = k.length - 1; i &gt;= 0; i--) {
            int tmp = currentMax * 10 + k[i];
            max = Math.max(max, find_max(n, k, tmp));
        }
        return max;
    }
}</code></pre>

https://www.acmicpc.net/problem/3085

• 분류 : 완전탐색

처음에 풀고나서 다른 사람들 풀이를 보고 기존에 제출했던 내 코드를 많이 뜯어고쳤다.

아래는 내가 처음 제출한 코드이다.

첫번째 풀이

• 반복문을 돌면서 swap()메서드로 인접한 사탕 위치(상하좌우)를 서로 바꿔서 clone된(swap된 배열) 배열을 리턴해준다. 그리고 그 swap된 배열을 countMaxCandyCount() 메서드로 행과 열을 체크하여 각 행과 열에 최대 사탕 개수를 찾는다.

import java.util.Scanner;

public class BOJ3085 {
    static char[][] arr;
    static int n;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt(); //  (3 ≤ N ≤ 50)
        sc.nextLine();
        arr = new char[n][n];
        for (int i = 0; i < n; i++) {
            String s = sc.nextLine();
            for (int j = 0; j < s.length(); j++) {
                arr[i][j] = s.charAt(j);
            }
        }
        findMax();
    }

    static private void findMax() {
        int max = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                //인접한 사탕 swap
                max = Math.max(countMaxCandyCount(swap(i, j, i, j - 1)), max);
                max = Math.max(countMaxCandyCount(swap(i, j, i, j + 1)), max);
                max = Math.max(countMaxCandyCount(swap(i, j, i + 1, j)), max);
                max = Math.max(countMaxCandyCount(swap(i, j, i - 1, j)), max);

            }
        }
        System.out.println(max);
    }

    static int countMaxCandyCount(char[][] clone) {
        if (clone == null) return -1;
        int max = 0;
        // row 체크
        for (int i = 0; i < n; i++) {
            int count = 1;
            for (int j = 0; j < n - 1; j++) {
                if (clone[i][j] == clone[i][j + 1]) count++;
                else count = 1;
                max = Math.max(max, count);
            }
        }

        // column 체크
        for (int i = 0; i < n; i++) {
            int count = 1;
            for (int j = 0; j < n-1; j++) {
                if (clone[j][i] == clone[j + 1][i]) count++;
                else count = 1;
                max = Math.max(max, count);
            }
        }
        return max;
    }

    static private char[][] swap(int i, int j, int a, int b) {
				//가장자리라서 상하좌우 위치가 유효하지 않은 경우
        if (a < 0 || a > n - 1 || b < 0 || b > n - 1) {
            return null;
        }
        // deep copy
        char[][] clone = new char[n][n];
        for(int x = 0; x<n; x++) {
            clone[x] = arr[x].clone();
        }

			  //swap 
        char tmp = clone[i][j];
        clone[i][j] = clone[a][b];
        clone[a][b] = tmp;

        return clone;
    }
}

수정한 코드

코드가 좀 지저분함을 스스로 느꼈다. 일단 굳이 swap한 배열을 clone해야하나? 싶기도 했고, 여러모로 리팩토링이 필요했다. 다른 사람들의 풀이를 참고해서 기존 코드를 아래와 같이 수정했다.

1. 상하좌우를 전체 다 swap하지 않고, 오른쪽과 아래쪽 값하고만 swap하도록 한다.

• 중복되는 swap 횟수를 줄였다. 어차피 arr[i][j-1]가 오른쪽에 있는 arr[i][j]와 swap하는 것과 arr[i][j]가 왼쪽에 있는 arr[i][j-1]와 swap하는게 동일하기 때문이다. 

2. swap할 때 굳이 deep copy를 해서 배열을 리턴하기보다는, swap 후 다시 원상복구해서 돌려놓는다. 그러면 매개변수로 굳이 배열을 넘길 필요가 없다.

• 위에서 언급했던 배열을 copy하는 부분을 제거했다. 배열을 복사하지 않고 swap후에 다시 되돌려놓으면(다시 swap해주면) 굳이 copy할 필요가 없기 때문이다.

import java.util.Scanner;

public class BOJ3085 {
    static char[][] arr;
    static int n;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt(); //  (3 ≤ N ≤ 50)
        sc.nextLine();
        arr = new char[n][n];
        for (int i = 0; i < n; i++) {
            String s = sc.nextLine();
            for (int j = 0; j < s.length(); j++) {
                arr[i][j] = s.charAt(j);
            }
        }
        findMax();
    }

    static private void findMax() {
        int max = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n - 1; j++) {
                // 인접한 사탕(오른쪽과 아래쪽) swap
                swap(i, j, i, j + 1);
                max = Math.max(findMaxCandyCount(), max);
                swap(i, j + 1, i, j); //swap했던걸 돌려놓음
            }
        }

        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < n; j++) {
                swap(i, j, i + 1, j);
                max = Math.max(findMaxCandyCount(), max);
                swap(i + 1, j, i, j);
            }
        }
        System.out.println(max);
    }

    static int findMaxCandyCount() {
        int max = 0;
        for (int i = 0; i < n; i++) {
            // row 체크
            int count = 1;
            for (int j = 0; j < n - 1; j++) {
                if (arr[i][j] == arr[i][j + 1]) count++;
                else count = 1;
                max = Math.max(max, count);
            }

            // column 체크
            count = 1;
            for (int j = 0; j < n - 1; j++) {
                if (arr[j][i] == arr[j + 1][i]) count++;
                else count = 1;
                max = Math.max(max, count);
            }
        }
        return max;
    }

    static private void swap(int i, int j, int a, int b) {
        char tmp = arr[i][j];
        arr[i][j] = arr[a][b];
        arr[a][b] = tmp;
    }
}

- 분류: 그리디 알고리즘

- 문제 링크 : https://www.acmicpc.net/problem/1931

풀이

최대한 많은 회의를 진행할 수 있도록 회의실을 사용하기 위해선 가장 빨리 끝나는 회의순으로 정렬하면 된다. 그러면 가장 많은 수의 회의가 회의실을 이용할 수 있게 된다.

다른 경우들을 살펴보자.

만약 회의가 가장 빨리 시작하는 순으로 정렬할 경우, 아래와 같은 반례가 존재한다. 회의가 가장 빨리 시작하는 순으로 회의실을 이용할 수 있게 할 경우 1개의 회의만이 회의실을 사용할 수 있지만, 최대 사용 가능 수는 3이다.

회의시간이 짧은 순으로 정렬할 경우는 아래와 같은 반례가 존재한다. 짧은 순으로 회의실을 이용할 수 있게 하면 아래의 경우는 1개 회의만이 회의실을 사용할 수 있게 되는데, 최대 2개의 회의가 이용 가능하기 때문이다.

그래서 회의가 가장 빨리 끝나는 순으로 회의실을 이용할 수 있게 해주면, 최대 수를 구할 수 있다.

그런데 여기서도 주의할 점이 있다.

회의를 빨리 끝나는 회의순으로 정렬할 때, 회의가 끝나는 시간이 같을 경우 시작시간이 빠른 순으로 정렬하도록 한다. 아래 그림을 보자. 회의가 끝나는 시간순으로 정렬할 때 시작시간을 고려하지 않으면 3개 회의(빨간색으로 체크한 부분)만이 회의실을 이용할 수 있게 된다.

import java.util.*;

public class Main {
	public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
        int result = 0;
        
        int count = sc.nextInt(); sc.nextLine();
        int meeting[][] = new int[count][2];
        
        for(int i = 0; i<count; i++) {
            meeting[i][0] = sc.nextInt();
            meeting[i][1] = sc.nextInt();
        }
        
        
        // 끝나는 시간 순으로 정렬 (오름차순)
        Arrays.sort(meeting, (o1, o2) -> {
			// 끝나는 시간이 같으면 시작시간이 빠른 순으로 정렬
            if(o1[1] == o2[1]) {
                return Integer.compare(o1[0], o2[0]);
            } else {
                return Integer.compare(o1[1], o2[1]);
            } 
        });
        
        
        int endTime = meeting[0][1]; // 가장 빨리 끝나는 시간
        result++;
        
        for(int i =  1; i<count; i++) {
            if(meeting[i][0] >= endTime ) {
                endTime = meeting[i][1];
                result++;
            } else {
                continue;
            }
        }
        
        System.out.println(result);
	}
}

[java] 2차원 배열 정렬하기

- Arrays.sort()

// 2차원 배열 정렬하기
public static void main(String[] args) {
//
  int[][] arr = {{1, 2}, {2, 3}, {3, 5}, {3, 4}};

  Arrays.sort(arr, (x, y) -> {
  if (x[0] == y[0]) { // 0번째가 같으면
  return x[1] - y[1]; // 1번째를 기준으로 오름차순
  }
  return x[0] - y[0]; // 0번째를 기준으로 오름차순
  });

  for (int i = 0; i < arr.length; i++) {
  System.out.println(arr[i][0] + " , " + arr[i][1]);
}

}

2019/10/08 - [JavaScript/초보자를 위한 자바스크립트] - 초보자를 위한 자바스크립트 커리큘럼

2019/10/14 - [JavaScript/초보자를 위한 자바스크립트] - +자바스크립트 - html과 css를 가볍게 알아보자!

2019/10/02 - [JavaScript/초보자를 위한 자바스크립트] - 1. 초보자를 위한 '자바스크립트는 무엇인가?' (feat.프로그래밍을 배우고 싶다면)

2019/10/08 - [JavaScript/초보자를 위한 자바스크립트] - 2. 자바스크립트 변수(variable)와 자료형(data type)

2019/10/14 - [JavaScript/초보자를 위한 자바스크립트] - 3. 자바스크립트 - 비교연산자(Comparisons)와 조건문(Conditional operators)

2019/11/19 - [JavaScript/초보자를 위한 자바스크립트] - 4. 자바스크립트 - 배열(Array)와 반복문(loop)

함수(Fuction)란?

이번 시간에는 자바스크립트(JavaScript)에서 '함수'에 대해 배워보도록 하겠습니다.

함수는 하나의 로직을 재실행할 수 있도록 하는 것입니다. 이러한 함수를 이용해서 반복되는 동일한 작업을 필요할 때마다 불러와서 사용할 수 있습니다. 이러한 것을 '코드 재사용'이라고 하기도 합니다. 한번 만들어둔 함수를 계속해서 불러와서 다시 사용할 수 있기 때문이죠.

함수는 1. 함수를 선언하기 2. 함수를 호출하기  ^[각주:1]이 두가지로 이루어집니다. 함수 선언 = 함수를 만든다고 볼 수 있고, 함수 호출 = 만들어둔 함수를 사용한다 라고 할 수 있습니다.

1. 함수 선언하기

function functionName( argument1, argument2, ...) {
	//do something
    }

2. 함수 호출하기

functionName( value1, value2, ...);

함수 예제 살펴보기

1. 덧셈 함수

function add(x, y) {
  document.write(x+y); //document.write는 화면에 x+y결과를 표시해준다.
}

add(2, 3);
add(2, 7);

위를 보면 x와 y라는 두 개의 인수(argument)값을 받아 더해주는 add라는 이름의 함수를 선언했습니다.

그리고 add(2,3); 이런식으로 더해줄 두 값을 넣어주면 add함수를 통해 더한 결과를 확인할 수 있습니다.

2. 1부터 n까지 더한 값을 구해주는 함수

function sum(x) {
  var result = 0;
  for(var i = 0; i<=x; i++){
    result += i; //result = i + result와 같다.
  }
  document.write(result);
}

sum(10);

지난 시간에 배운 반복문을 이용하여 이런 식의 함수를 만들어볼 수도 있습니다.

한개의 값(x)을 받아서 1부터 해당 값까지 모두 더한 값을 출력하는 함수입니다.

10을 입력받으면 1부터 10까지 더한 값을 출력해주는 것입니다.

버튼 클릭 이벤트(Button Click Event)

자바스크립트에서 함수는 '버튼 클릭 이벤트를 발생'시킬 때도 자주 사용합니다.

예를 들어 사용자가 버튼을 클릭했을 때 "안녕?"이라는 alert창을 띄우고 싶다고 합시다. 이때 버튼을 누르는 사용자의  행위(action)를 이벤트(event)라고 합니다.  그리고 이 이벤트에 맞춰서 발생할 동작을 함수로 구현할 수 있습니다.

*이벤트(event) : 이벤트(event)는 사용자의 행위(action)를 의미합니다. 즉 사용자가 버튼을 누르거나 브라우저를 닫거나 하는 것들을 이벤트라고 볼 수 있습니다. 위의 예시에서는 버튼을 클릭하는 행위를 이벤트로 볼 수 있습니다.

*이벤트 타입(event type) : 이벤트의 종류를 의미합니다. 예를 들어 버튼을 클릭하는 이벤트라고 하면 click이 그 이벤트 타입입니다. 이밖에도 다양한 종류의 이벤트 타입이 존재합니다. ^[각주:2]

*이벤트 타겟(event target): 이벤트가 일어날 객체^[각주:3]를 의미합니다. 예를 들어서 id가 A라는 버튼을 클릭했을 때 이벤트가 발생하도록 하고 싶은 거라면 A라는 버튼이 타겟이 되는 것입니다.

*이벤트 핸들러(event handler) = 이벤트 리스너(event listener) : 이벤트가 발생했을 때 동작하는 코드를 의미합니다. ^[각주:4]

1. 사용자가 버튼을 클릭했을 때 "안녕?"이라는 alert창을 띄우는 예제

  <button id = "btn1">버튼</button>

버튼생성과 같은 content나 구조에 대한 것은 html로 작업합니다.

codesandbox를 켜서 html파일에 위와 같이 적어주면 웹페이지에 버튼이 생성된 것을 확인할 수 있습니다.

document.getElementById("btn1").addEventListener('click',hello);

function hello(){
  alert("안녕?");
}

 버튼에 대해 '동작'하는 부분은 javascript가 담당합니다. 

2. 숫자 n을 입력받아 1부터 n까지 더한 결과를 출력하는 함수 만들기

이는 보다 심화된 예제입니다.

<input id="number" /> 
    <button id="btn1" onclick="addNum();">입력</button>
    <br />
    결과: <span id="output"></span>

먼저 html에는 숫자를 입력받을 창과 누르면 결과를 출력하도록 하는 버튼, 그리고 결과를 출력하는 부분 총 3가지가 필요합니다.

입력받는 것은 input태그^[각주:5]를 이용하여 만들 수 있습니다. 그리고 버튼은 button태그를 이용하고, 결과를 띄워주기 위해 span태그를 이용해보도록 하겠습니다. (이때 div태그를 이용해도 괜찮습니다. 일단은 자세한 설명은 생략하고 사용하면서 어떤식으로 이용하는건지 익혀보도록 하겠습니다.) ^[각주:6]

document.getElementById("btn1").addEventListener("click", addNum);

function addNum() {
  var result = 0;
  var num = document.getElementById("number").value;
  for (var i = 1; i <= num; i++) {
    result += i; // result = result + i 와 같다.
  }

  document.getElementById("output").innerHTML = result;
}

 javascript파일에는 버튼을 클릭하는 이벤트가 발생했을 때 실행될 부분을 적어주어야합니다.

<코드설명>

*getElementById() : id를 이용하여 특정한 값을 가진 요소를 가져옵니다.

위에 코드를 보면 html파일의 button태그에 btn1이라는 id값을 주었습니다. 만약 버튼(button)이 여러개이고, 이중에서 하나의 버튼에 대해서만 특정 함수가 작동하길 바란다면 그 특정 버튼에 id값을 주어 다른 버튼들과 구분할 수 있습니다.

*addEventListener(): 이벤트 리스너는 특정 이벤트가 발생했을 대 그 처리를 담당하는 함수를 가리킵니다. addEventListener는 특정 이벤트 발생시 특정 함수를 실행시킵니다.

document.getElementById("btn1").addEventListener("이벤트종류", 함수이름);

우리가 작성할 이벤트리스너는 사용자가 버튼을 클릭했을 때 발생하므로 이벤트 종류는 click이고, 함수이름은 저는 addNum으로 설정했습니다.

*document.getElementbyId("아이디").innerHTML : 해당 id를 가진 객체 영역에 html코드를 삽입하는 소스입니다.

<div id = "test">김커피</div>

document.getElementById("test").innerHTML = "김라떼로 개명!";

위와 같은 예제를 직접 작성해보면 innerHTML이 어떤식으로 쓰이는지 알 수 있을겁니다 :)